How Do You Find the Midpoint of Two Coordinates
Geometry has a funny way of making simple things sound complicated. You are staring at a piece of graph paper or a screen with two random dots, labeled something like A and B, and you are asked to find the exact middle.
At first glance, it feels abstract. You might be tempted to just eyeball it and say, “It looks like it’s right about there.” But in math, “looks like” isn’t good enough. You need precision. You need coordinates.
The good news is that finding the middle of two points is actually one of the most intuitive things you will do in geometry. It isn’t about complex calculus or memorizing a dictionary of rules. It is essentially just finding an average. If you can average two test scores, you can find a midpoint.
In this guide, we will cover how to find the midpoint of two coordinates, the exact formula used, step-by-step examples, and how to use our free midpoint calculator with graph.
Don’t want to do the math by hand? Use our free midpoint calculator below to instantly find the midpoint of two coordinates and see it plotted clearly on a graph.
Midpoint Calculator
Just enter the coordinates of the two points to get the result instantly.
Coordinates Input
Calculation Results
Ready to Calculate
Enter coordinate values on the left to see the result, steps, and graph here.
- How Do You Find the Midpoint of Two Coordinates
- What Is the Midpoint of Two Coordinates?
- Why Finding the Midpoint Matters
- Real World Uses of the Midpoint Formula
- The Midpoint Formula
- Step-by-Step: How Do You Find the Midpoint of Two Coordinates Manually
- Worked Examples (With Interpretation)
- Visualizing the Midpoint on a Graph
- How to Find the Midpoint Without a Formula (Visual Logic)
- Special Cases You Should Know
- Common Mistakes to Avoid
- How to Use Our Midpoint Calculator
- Midpoint vs Distance vs Slope – Quick Comparison
- Frequently Asked Questions About Finding the Midpoint
- Summary
- Related Calculation: How to Find the Distance Between Two Coordinates
- Disclaimer
What Is the Midpoint of Two Coordinates?
Before we dive into the math, let’s clarify what the midpoint actually represents.
In the simplest terms, the midpoint is the halfway point. Imagine a piece of string stretched tight between two nails. If you were to take a pair of scissors and cut that string exactly in the center so that both pieces were perfectly equal in length, that cut point is your midpoint.
In the world of coordinate geometry, we are working on a grid (the Cartesian plane). We have two endpoints that define a line segment. The midpoint is the specific coordinate (x,y) that sits on that line segment and is equidistant from both endpoints. It is the center of balance.
If you were walking in a straight line from Point A to Point B, the midpoint is the exact moment you have walked half the distance and have half the distance left to go. It splits the journey—and the line segment—into two equal halves.
Why Finding the Midpoint Matters
You might be asking yourself, “Why do I actually need to know how to find the midpoint of two points?” Aside from passing your next math quiz, this concept is a building block for much larger ideas in geometry and real-life analysis.
Here is why it is important:
- Solving Coordinate Geometry Problems: It is often the first step in more complex problems, like finding the perpendicular bisector of a line (a line that cuts another line in half at a 90-degree angle).
- Finding Centers: If you have the two endpoints of the diameter of a circle, the midpoint is the center of that circle. This is crucial for writing the equation of a circle.
- Graphing and Visual Verification: When you are plotting data or drawing shapes, knowing the midpoint helps you keep your drawings accurate and symmetrical.
- Foundation for Slope and Equations: Understanding where the middle is helps in understanding the steepness (slope) and the overall behavior of lines on a graph.
It essentially gives you a reference point. In a sea of infinite coordinates, the midpoint anchors you right in the center of the action.
Real World Uses of the Midpoint Formula
Math often feels stuck on the chalkboard, but the concept of a midpoint appears everywhere in the physical world. Understanding how to calculate the midpoint of two coordinates turns abstract numbers into real, practical meaning.
Here are a few ways this logic applies outside of the classroom:
- Civil Engineering and Construction: When engineers plan a bridge, they need to know the exact center of the span to calculate load distribution. If a beam connects two pillars, the midpoint is where the stress might be calculated differently, or where a support cable needs to anchor.
- Computer Graphics and Design: Every time you use a design tool to “center” an image or text between two other objects, the software is running a midpoint calculation in the background. It takes the coordinates of the edges and calculates the exact middle pixel to place your object.
- Urban Planning and Mapping: If a city planner wants to build a fire station or a school that serves two distinct neighborhoods equally, they might look for the geographic midpoint between the centers of those two populations to minimize travel time for everyone.
- Physics and Motion: If you are analyzing the trajectory of an object, knowing the midpoint of its path can help determine average velocity or the peak height of a projectile in certain symmetric motion scenarios.
The Midpoint Formula
Now, let’s look at the math. The beauty of the midpoint formula is that it is incredibly logical.
If you want to find the middle number between 10 and 20, what do you do? You average them: 10 + 20 = 30, and 30 / 2 = 15.
The midpoint formula does the same thing twice—once for the x-values (horizontal) and once for the y-values (vertical)
The Formula
M = ( (x₁ + x₂) ÷ 2 , (y₁ + y₂) ÷ 2 )
Here is what the symbols mean:
- M represents the Midpoint.
- x₁ and y₁ are the coordinates of the first point.
- x₂ and y₂ are the coordinates of the second point.
The Logic:
- Average the x-values: You add the two x-coordinates together and divide by 2. This gives you the horizontal center.
- Average the y-values: You add the two y-coordinates together and divide by 2. This gives you the vertical center.
That’s it. There are no squares, no square roots, and no complex trigonometry. You are just finding the average of the coordinates.
Step-by-Step: How Do You Find the Midpoint of Two Coordinates Manually
Let’s break this down into a repeatable process. Whenever you are asked to find midpoint between two points, you can follow these four steps to get the answer right every time.
Step 1: Write Down and Label the Coordinates
First, simply write down the two points you are given. Label the first one (x₁, y₁) and the second one (x₂, y₂). It doesn’t matter which one is first or second; the math works out the same.
- Point A: (2, 4)
- Point B: (6, 10)
Step 2: Add the x-Coordinates
Take the first number from each pair (the x’s) and add them together.
- 2 + 6 = 8
Now, divide that result by 2.
- 8 ÷ 2 = 4
This is the x-coordinate of your midpoint.
Step 3: Add the y-Coordinates
Take the second number from each pair (the y’s) and add them together.
- 4 + 10 = 14
Now, divide that result by 2.
- 14 ÷ 2 = 7
This is the y-coordinate of your midpoint.
Step 4: Write the Midpoint as an Ordered Pair
Combine the values you found in steps 2 and 3 into a final coordinate pair (x, y).
- Midpoint M = (4, 7)
Worked Examples (With Interpretation)
To really master how do you find the midpoint of two coordinates, it helps to look at different scenarios. We will look at simple positive numbers, negative numbers, and decimals.
Example 1: Positive Coordinates
The Scenario: You have a line segment on a graph with two endpoints: A (4, 8) and B (12, 16). You need to find the exact center.
The Math:
- Add x’s: 4 + 12 = 16
- Divide x by 2: 16 ÷ 2 = 8
- Add y’s: 8 + 16 = 24
- Divide y by 2: 24 ÷ 2 = 12
Answer: The midpoint is (8, 12).
Interpretation: This point lies exactly in the middle of the segment connecting A and B. Think of it like a staircase: to get from A to B, you go “up and over.” The midpoint is exactly halfway up and halfway over. If you graphed it, it would be 4 units in each direction away from A and B
Example 2: Negative Coordinates (Watch Your Signs!)
The Scenario: You are working with points in different quadrants. One point is P (-5, 2) and the other is Q (3, -6). Note: This is where most mistakes happen—be careful when adding negative numbers.
The Math:
- Add x’s: -5 + 3 = -2
- Divide x by 2: -2 ÷ 2 = -1
- Add y’s: 2 + (-6) = -4
- Divide y by 2: -4 ÷ 2 = -2
Answer: The midpoint is (-1, -2).
Interpretation: Even though the endpoints are far apart in different sections of the graph, the formula works perfectly. The math tells us the “balance point” is in the third quadrant (bottom-left), where both coordinates are negative.
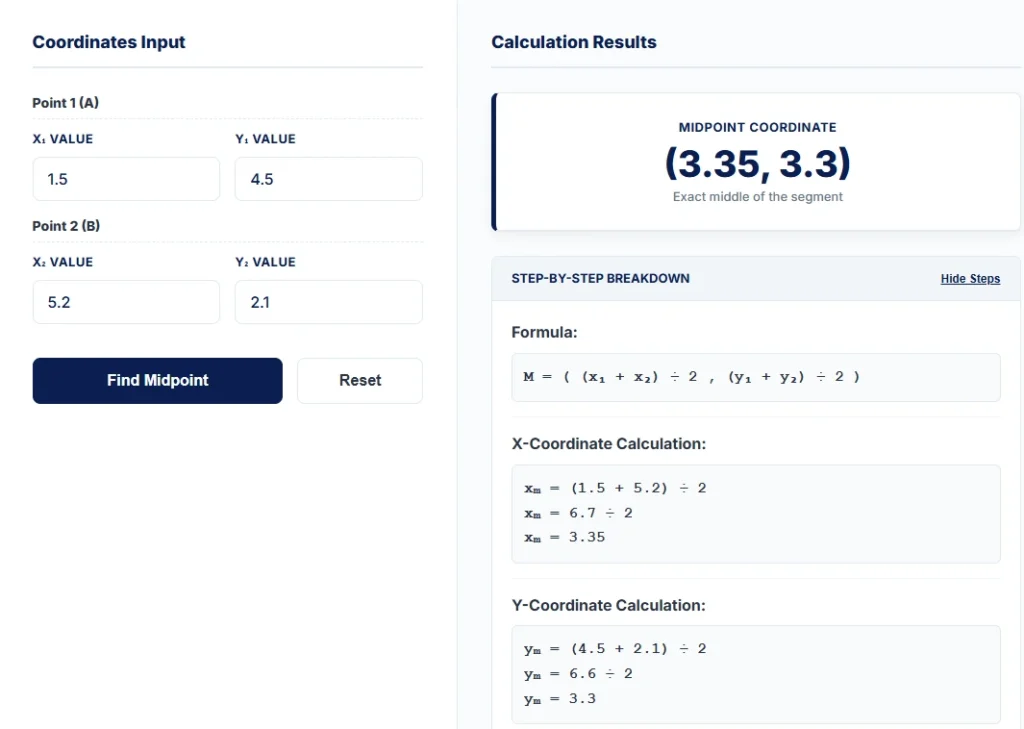
Example 3: Decimal Coordinates
The Scenario: Real world data is rarely perfect. Suppose you have two GPS coordinates or measurements: X (1.5, 4.5) and Y (5.2, 2.1).
The Math:
- Add x’s: 1.5 + 5.2 = 6.7
- Divide x by 2: 6.7 ÷ 2 = 3.35
- Add y’s: 4.5 + 2.1 = 6.6
- Divide y by 2: 6.6 ÷ 2 = 3.3
Answer: The midpoint is (3.35, 3.3).
Interpretation: Midpoints are not always whole numbers (integers). If you are measuring distance or building a physical object, you will often end up with decimals. This result is perfectly valid and precise.
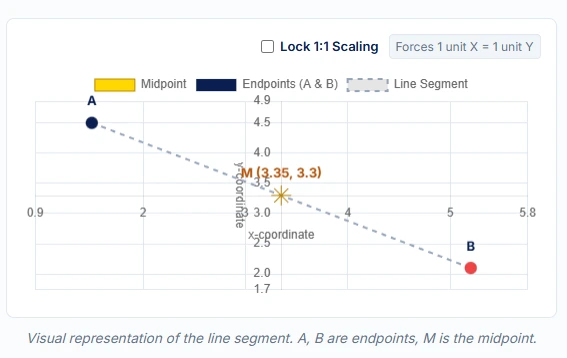
Visualizing the Midpoint on a Graph
Sometimes, numbers on a page can feel disconnected from reality. It is helpful to visualize what is happening on the graph.
Imagine drawing a straight line connecting your two points. That line has a specific length and a specific direction. The midpoint is the exact center of that line segment.
If you look at the midpoint on a graph, you can visually verify your answer using a “staircase” method:
- Count how many units you have to move horizontally to get from Point A to Point B (the run).
- Count how many units you have to move vertically (the rise).
- To get to the midpoint, you simply move half that horizontal distance and half that vertical distance starting from either point (A or B).
For example, if moving from point A to point B requires going 10 units to the right and 6 units upward, then the midpoint is reached by moving half that distance: 5 units to the right and 3 units upward from point A.
The graph in our calculator above is designed to show you this relationship instantly. You will see the two endpoints in one color (usually distinctive) and the midpoint typically highlighted (like a star or a different color dot) right in between them.
Quick Visual Check
- The midpoint must lie exactly halfway on the line segment.
- The horizontal and vertical distances from each endpoint to the midpoint should be equal.
How to Find the Midpoint Without a Formula (Visual Logic)
What if you forget the midpoint formula during a test? Or what if you just hate memorizing formulas? You can actually find the answer using visual logic and common sense.
Think of the midpoint as the ‘middle value’ on a number line, found by averaging two numbers.
The “Number Line” Method:
- Look at the X values only: Imagine them on a ruler. If one point is at 2 and the other is at 10, ask yourself: “What number is exactly in the middle of 2 and 10?”
- You might count up from 2 and down from 10 until you meet in the middle.
- 3, 4, 5… 6 … 7, 8, 9.
- 6 is the middle. That is your x-coordinate.
- Look at the Y values only: Do the same thing. If the y-values are 4 and 12, what is in the middle?
- The distance between 4 and 12 is 8. Half of 8 is 4.
- So, start at 4 and add 4. You get 8. That is your y-coordinate.
This method works because the midpoint formula is just a fancy way of saying “average.” By treating the horizontal and vertical distances separately, you can often solve these problems in your head without writing down a single equation. It is a great way to double-check your work!
Special Cases You Should Know
While the standard formula works for everything, there are a few special scenarios where you don’t even need to do the math if you recognize the pattern.
1. Vertical Lines
If the two x-coordinates are the same e.g., (3,5) and (3,15), the line is vertical.
- The trick: The x-coordinate of the midpoint will be the same (3). You only need to find the middle of the y-values (5 and 15).
- Midpoint: (3,10).
2. Horizontal Lines
If the two y-coordinates are the same e.g., (2,8) and (10,8), the line is horizontal.
- The trick: The y-coordinate of the midpoint will be the same (8). You only need to find the middle of the x-values (2 and 10).
- Midpoint: (6,8).
3. Identical Points
If Point A is (5,5) and Point B is also (5,5), where is the midpoint?
- It is the point itself: (5,5). The distance is zero, so the middle is just the point you are standing on.
Common Mistakes to Avoid
Even though the math is simple addition and division, it is easy to make silly errors. Here are the most common pitfalls students encounter when learning how to find the midpoint of two coordinates.
1. Subtracting instead of Adding
- The Mistake: Confusing the midpoint formula with the distance or slope formulas (which use subtraction). You might accidentally calculate (x₂ – x₁) / 2.
- The Fix: Remember, you are finding an average. To find an average, you always add the items first. Think “Add and Divide.”
2. Mixing up X and Y
- The Mistake: Adding an x-coordinate to a y-coordinate, like (x₁ + y₁) / 2.
- The Fix: Keep your x’s and y’s in separate lanes. X goes with X; Y goes with Y.
3. Forgetting to Divide by 2
- The Mistake: Doing the addition but forgetting the division step, resulting in a coordinate that is way off the graph.
- The Fix: Always ask yourself, “Does this answer make sense?” If your endpoints are (2, 2) and (4, 4) and your answer is (6, 8), you know visually that the answer is way too big.
4. Sign Errors with Negatives
- The Mistake: When adding a negative number (e.g., 5 + -3), treating it as regular addition (5 + 3 = 8) instead of subtraction (5 – 3 = 2).
- The Fix: Use a calculator or write it out clearly. Remember that 5 + (-3) is exactly the same as 5 – 3.
How to Use Our Midpoint Calculator
While calculating the midpoint by hand is essential for learning, a calculator becomes especially useful when working with decimals, negative numbers, or when you want to quickly check your homework.
We built the midpoint calculator above as a reliable tool for both calculation and visualization. It handles all the arithmetic automatically and plots the result on a graph instantly.
Follow these steps to get the most out of the calculator:
- Enter Point 1 (A):
In the left-hand column (or the top section on mobile), locate the Point 1 input area. Enter the values for x₁ and y₁. - Enter Point 2 (B):
Just below Point 1, enter the coordinates x₂ and y₂ for the second point. - Automatic Calculation:
The calculator begins processing as you type. If needed, you can click the Find Midpoint button to trigger the calculation manually and clear any error messages. - View the Result:
The result panel on the right (or at the bottom on mobile) displays the exact midpoint coordinates clearly and prominently. - Check the Steps:
Below the main result, you’ll find a Step-by-Step Breakdown section. Click Show Steps to see the full calculation, including the addition and division used to find the midpoint. This is especially helpful for learning and verification. - Analyze the Graph:
The graph plots both endpoints in contrasting colors and highlights the midpoint with a distinct marker, making it easy to confirm that the point lies exactly halfway between them.
Tip:
Enable the Lock 1:1 Scaling option above the graph. This keeps the grid perfectly square, ensuring that horizontal and vertical distances appear visually accurate (graphs can otherwise stretch to fit the display area).
Midpoint vs Distance vs Slope – Quick Comparison
| Concept | What It Finds | What the Formula Does | Type of Result | Example Result |
| Midpoint | A location (the exact center between two points) | Averages the coordinates (addition ÷ 2) | An ordered pair (x, y) | (3, 5) |
| Distance | A length (how far apart the points are) | Uses subtraction, squaring, and a square root (Pythagorean theorem) | A single number | 5 units |
| Slope | A rate of change (how steep the line is) | Divides vertical change by horizontal change (rise ÷ run) | A number or ratio | 1/2 or 3 |
Key takeaway:
The midpoint is the only one that gives a coordinate pair as the answer.
Both distance and slope produce a single value, not a point.
Frequently Asked Questions About Finding the Midpoint
Summary
- Finding the midpoint is all about balance. No matter the situation—whether you’re analyzing a graph, planning a design, or finishing a homework problem—you’re simply locating the point that sits exactly halfway between two others.
- Once you understand that the midpoint is found by averaging the horizontal and vertical positions separately, the idea becomes intuitive rather than mechanical. The same reasoning works for positive numbers, negatives, and decimals alike.
- When you want to move faster or confirm your answer visually, you can always use the midpoint calculator above. Seeing the midpoint plotted between the two endpoints is a quick and reliable way to build confidence and make sure your result truly sits in the center.
Related Calculation: How to Find the Distance Between Two Coordinates
The midpoint shows where the center of a line lies, but distance tells you how far apart the two endpoints are. If you want to measure the actual length between two coordinates, see our guide on how to find and calculate the distance between two coordinates.
Disclaimer
This content and the embedded midpoint calculator are provided for educational and informational purposes only. While every effort is made to ensure mathematical accuracy, the results may not be error-free and should not be relied upon for critical professional applications such as engineering, construction, surveying, or navigation. We assume no responsibility or liability for any errors, omissions, or outcomes resulting from the use of this content or tool.
