How to Calculate the Area of an Irregular Shape

Let’s be honest: measuring a perfect square or a simple rectangle is easy. You just grab a tape measure, multiply the length by the width, and you are done.

But the real world is rarely built in perfect straight lines. Whether you are a homeowner trying to figure out how much sod you need for a curvy backyard, a student staring at a complex geometry problem, or a contractor estimating flooring for a room with weird nooks and crannies, you have likely asked yourself: how to calculate the area of an irregular shape?

It looks intimidating because there isn’t a single “magic button” or one-size-fits-all formula like there is for a circle. But don’t worry—it is not impossible. In fact, it is actually quite satisfying once you break it down.

In this guide, we will cover exactly how to find the area of an irregular shape, the specific formulas you can use, and how to use our free tool for accurate results.

Don’t want to do the math manually? Use our free tool below to get an instant answer using Decomposition, Grid Counting, or Coordinates.

Irregular Shape Area Calculator

Before we figure out how to calculate the area of an irregular shape, we need to agree on what one actually is.

In the world of geometry, a “regular” shape is the teacher’s pet. It follows all the rules. A regular polygon (like a square or an equilateral triangle) has sides that are all the same length and interior angles that are all the same size. They are predictable.

An irregular shape is the rebel. It is any 2D closed figure where:

• The sides are not equal lengths.
• The angles are strictly not equal.
• It might not even have straight sides (think of a kidney-bean-shaped swimming pool).

Common Examples

• Plot of Land: Property lines rarely form perfect squares; they often follow roads or creeks.
• Odd-Shaped Room: An L-shaped living room or a kitchen with a bay window.
• Polygons with Unequal Sides: A pentagon where every side is a different length.
• Naturally Occurring Shapes: A leaf, a pond, or a spill.

Why Is This Important?

Knowing how do I calculate the area of an irregular shape is a critical skill in many industries:

• Education: Understanding that math applies to the messy, real world, not just textbook examples.
• Construction: Estimating concrete for a custom patio.
• Landscaping: Ordering the exact amount of mulch so you don’t waste money.
• Architecture: Designing spaces that fit into existing, awkward boundaries.

Depending on the shape you are looking at and the data you have available, there are three main methods to solve this puzzle.

Method 1: The Decomposition Method (Divide and Conquer)

This is the most common method used in construction, flooring, and DIY projects. When people ask, “how do I calculate the area of an irregular shape with straight edges?”, this is usually the answer.

The Concept

Imagine you have a weirdly shaped room. You can’t multiply “length times width” because there isn’t just one length. But, if you draw a line across the room, you might suddenly see two rectangles. Decomposition is simply the fancy math term for “cutting it up”. You split your complex irregular polygon into shapes you recognize: squares, rectangles, triangles, or semicircles.

How to Do It Step-by-Step

1. Sketch the Shape: Draw the outline of your irregular shape on paper.
2. Draw “Cut Lines”: Look for natural places to divide the shape. Can you draw a vertical line that turns an L-shape into two rectangles? Can you slice a corner off to make a right-angled triangle?
3. Measure the New Parts: Now that you have, say, two rectangles and one triangle, measure the specific height and width of those individual parts.
4. Calculate Individually: Find the area of each small part.
   • Rectangle: Length x Width
   • Triangle: 0.5 x Base x Height
5. Sum It Up: Add all those small areas together to get the total area of irregular shape.

Tip: The Subtraction Method

Sometimes, it is easier to add than to divide. Imagine a square piece of paper with a corner cut off. Instead of measuring the weird shape, calculate the area of the full square as if the corner was still there, calculate the area of the missing triangular corner, and subtract the triangle from the square. Our calculator supports this via the “Sub (-)” feature.

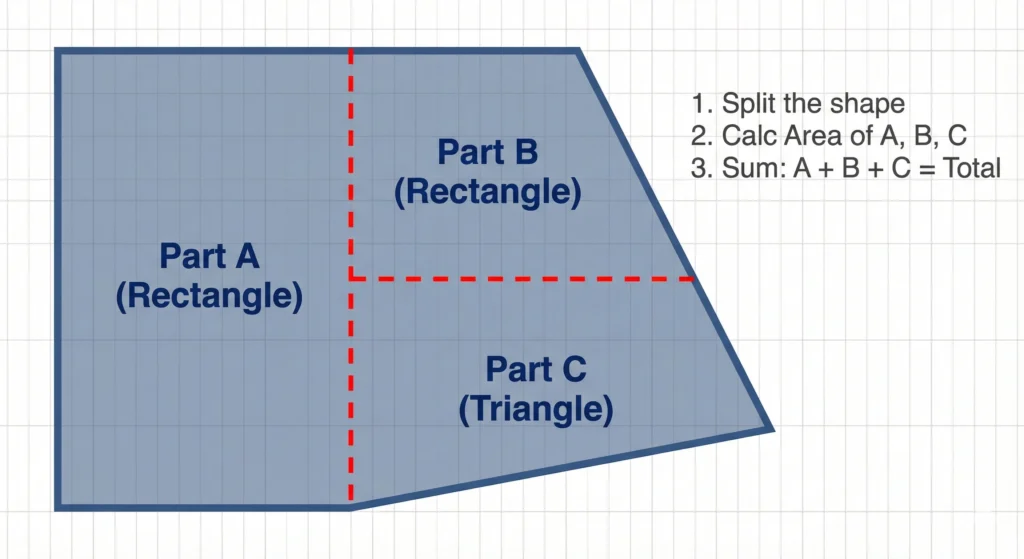
A geometric diagram illustrating the Decomposition Method. An irregular L-shaped polygon is divided by red dashed lines into three simpler shapes: Part A (a rectangle), Part B (a rectangle), and Part C (a triangle). Text on the right lists the process: 1. Split the shape, 2. Calculate the area of parts A, B, and C, and 3. Sum them to find the total area.

Method 2: The Grid Counting Method (Best for Curves)

What if your shape doesn’t have straight lines? What if you are trying to find the area of an irregular shape like a pond, a leaf, or a spill? You can’t cut a cloud into perfect triangles. This is where the Grid Method comes in. It is less about perfect formulas and more about smart estimation.

The Concept

If you draw your shape on graph paper, the graph paper itself becomes your measuring tool. Since you know the area of one tiny square on the grid, you just need to count how many squares the shape covers.

How to Do It Step-by-Step

1. Overlay a Grid: Place a transparent grid over your shape, or draw the shape onto graph paper.
2. Define Your Scale: Determine what one square represents. For example, if your grid squares are 1cm x 1cm, then one square = 1 cm².
3. Count Full Squares: Go through and count every square that is completely inside the shape.
4. Count Partial Squares: Now count the squares that are only partially covered by the border of your shape.
5. The “Half-Square” Rule: The standard rule of thumb is to treat every partial square as 0.5 (half). Some will be mostly full, some mostly empty, but they tend to even out.

The Formula

Total Area = (Count of Full Squares) + (Count of Partial Squares x 0.5)

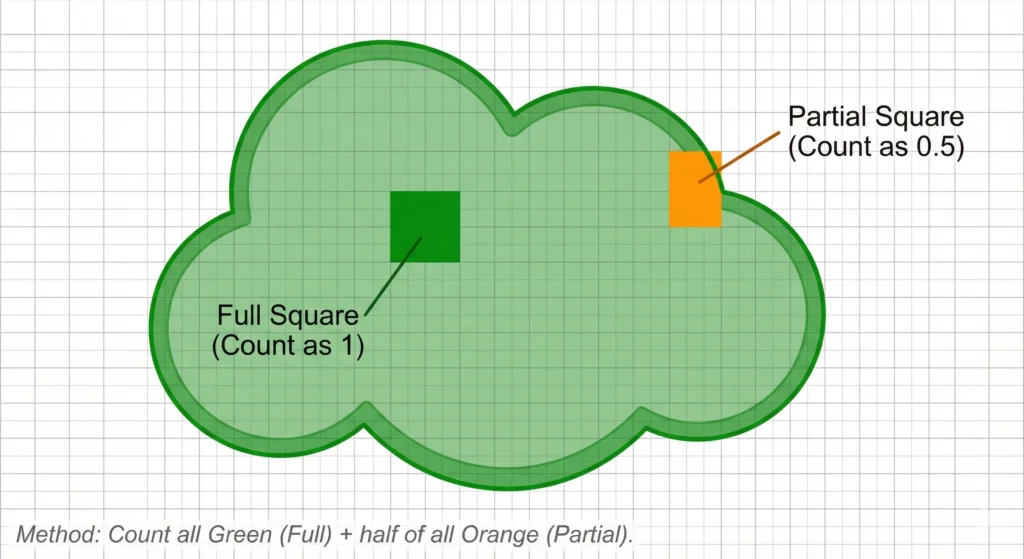
A diagram visualizing the Half-Square Rule for estimating the area of curved shapes. An irregular organic shape overlays a square grid. One fully covered square is highlighted in green and labeled “Count as 1.” A partially covered square is highlighted in orange and labeled “Count as 0.5.” The caption explains the formula: “Count all Green (Full) + half of all Orange (Partial).”

Method 3: Coordinate Geometry (The Shoelace Formula)

This method is the heavy hitter. It is what professional land surveyors and engineers use. If you want to know how do you find the area of an irregular polygon with pinpoint precision, this is the way. You don’t need to physically measure every inch of the perimeter; you just need the coordinates (x,y) of each corner (vertex).

What is the Shoelace Formula?
It is called the “Shoelace Formula” (or Surveyor’s Formula) because when you write the coordinates down in a list and cross-multiply them, the pattern looks like the laces on a shoe.

How it Works (Simplified)
Let’s say you have a shape with corners at three points: A(x1, y1), B(x2, y2), and C(x3, y3).

1. List the Coordinates: Crucial Rule: You must list them in order, moving around the shape either clockwise or counter-clockwise.
2. Repeat the First Point: Add the first point (A) again at the bottom of the list.
3. Multiply Diagonally Right:  (x × next y) and add them up.
4. Multiply Diagonally Left: (y × next x) and add them up.
5. Calculate: Subtract the second sum from the first sum, take the absolute value, and divide by 2.

The Irregular Polygon Area Formula
Area = 1/2 | (x₁y₂ + x₂y₃ + …) − (y₁x₂ + y₂x₃ + …)

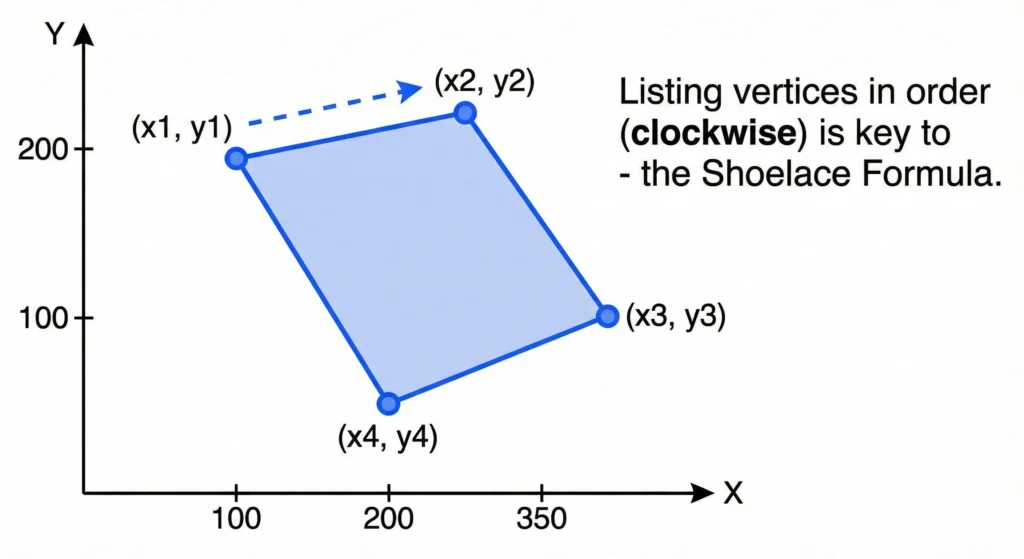
A mathematical graph showing a polygon plotted on an X and Y axis. The polygon’s four vertices are marked with blue dots and labeled with coordinates (x1, y1) through (x4, y4). A dashed blue arrow indicates a clockwise path connecting the points. Side text notes that listing vertices in order is key to using the Shoelace Formula for area calculation.

Still unsure how to calculate the area of an irregular shape for your specific project? Here is a quick cheat sheet:

Scenario	Best Method	Why?
School Math Problems	Any	If given vertices (x,y), use Coordinates. If given side lengths, use Decomposition.
Home Renovation (Flooring, Painting)	Decomposition	Rooms are usually combined rectangles. Easy to measure with a tape.
Landscaping / Gardening	Grid Counting	Flower beds and ponds are curved. Precision isn’t critical, but a good estimate is needed.
Land Surveying	Coordinates	You need exact legal boundaries and often have GPS points.

When calculating area, it is important to understand exactly what is being measured. This avoids errors in planning, analysis, material estimation, or academic work.

✅ Included:

The Shape Outline: Everything inside the defined boundary.

Measurable Sides: Any straight edge you can measure with a tape.

Coordinates: If using the coordinate method, every vertex contributes to the final area.

❌ Excluded:

Holes or Cutouts: Unless you specifically subtract them (using the Decomposition method), the math assumes the shape is solid.

3D Elements: This is strictly for 2D area (square footage). It does not calculate volume (cubic footage).

Assumptions: The formulas do not “guess” missing sides. You must measure the entire perimeter or define the grid.

If you are doing this manually, follow this roadmap to ensure you don’t get lost in the numbers.

Step 1: Choose a Method

Look at your shape. Does it have straight lines? Use Decomposition or Coordinates. Is it curvy or organic (like a lake)? Use Grid Counting.

Step 2: Measure Your Shape

• Decomposition: Get your tape measure out. Measure every straight edge. Split the shape mentally and measure the “invisible” lines that divide your rectangles and triangles.
• Coordinates: Set a “0,0” point (origin) and measure the distance of every corner from that point.
• Grid: Find a transparent grid overlay or draw one on paper.

Step 3: Apply the Formula or Count

• Decomposition: Calculate L × W  for rectangles and 0.5 × B × H for triangles. Add them up.
• Coordinates: Plug your (x,y) points into the Shoelace formula (or our calculator).
• Grid: Count full squares + (partial squares × 0.5).

Step 4: Compare / Verify

Does the answer make sense? If you calculated a small bedroom is 5,000 square feet, something went wrong. Always double-check your math or use a second method to verify.

Even with the best formulas, small errors can lead to big problems. Here are the most common pitfalls when learning how to find the area of an irregular shape.

• Mixing Units: Never multiply feet by inches. If one side is 10 feet and another is 6 inches, convert them both to feet (10 ft and 0.5 ft) before calculating.
• Listing Coordinates Out of Order: When using the Shoelace formula, you must list points in consecutive order around the perimeter (clockwise or counter-clockwise). If you “jump” across the shape, the formula breaks.
• Ignoring Holes: If your room has a kitchen island or a pillar in the middle, remember to calculate that area separately and subtract it from your total. The standard decomposition method assumes the space is empty.
• Miscounting Partial Squares: In the Grid Method, it is tempting to guess “this one is 0.9 full” and “this one is 0.1 full.” Stick to the rule: every partial square counts as 0.5. It saves time and averages out accurately.

The following examples show how area calculations apply in academic problems, professional work, and real-world situations.

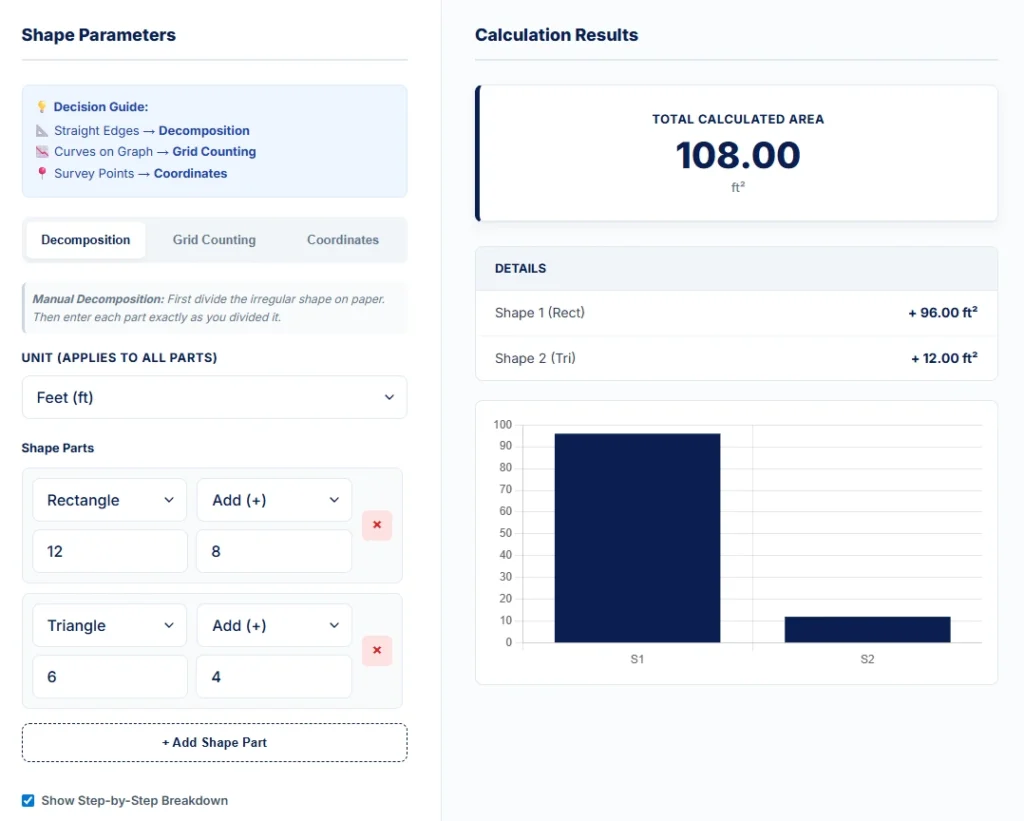
Example A: Irregular Room Layout (Decomposition Method)

Scenario
An L-shaped room can be divided into simpler shapes. The main rectangular section measures 12 by 8 units, and the attached section forms a right-angled triangle with a base of 6 units and a height of 4 units.

Calculation
Rectangle area = 12 × 8 = 96 square units
Triangle area = (6 × 4) ÷ 2 = 12 square units

Total Area
96 + 12 = 108 square units

Interpretation
This method is well-suited for classrooms, architectural planning, interior design, and construction tasks such as estimating flooring, paint coverage, or usable space.

Example B: Irregular Surface Area (Grid Counting Method)

Scenario
An irregular shape is drawn on graph paper, where each grid square represents 1 square unit. The shape covers 150 full squares and approximately 20 partial squares.

Calculation
Estimated area = 150 + (20 × 0.5)
Estimated area = 160 square units

Interpretation
Grid counting provides a reliable approximation for academic exercises, environmental studies, landscaping layouts, and preliminary planning where exact boundaries are difficult to measure.

Example C: Area from Known Coordinates (Shoelace Formula)

Scenario
A polygon is defined by four vertices with known coordinates:
(0, 0), (4, 0), (4, 3), and (0, 4).

Method
The area is calculated using the Shoelace (Surveyor’s) Formula, which uses coordinate pairs instead of physical measurements.

Result
Calculated area = 14 square units

Interpretation
This method is widely used in mathematics, surveying, engineering, and geographic analysis. It offers high precision when accurate coordinate data is available and minimizes errors associated with manual angle or distance measurement.

The calculator shown above is designed to handle the calculations for you. Follow the steps below to get accurate and reliable results.

1. Select a Method
 Use the tabs to switch between Decomposition (combining simple shapes), Grid Counting (approximation), or Coordinates (vertex-based calculation).

2. Enter Your Data

• Decomposition: Choose a shape, such as a rectangle, and enter its dimensions. Use “Add Shape” to include additional sections.
• Grid Counting: Enter the number of full and partial grid squares.
• Coordinates: Input the X and Y values for each corner in sequence, moving clockwise or counter-clockwise.

3. Review the Breakdown
Enable “Show Step-by-Step Breakdown” to see how the final area is calculated.

4. Confirm Visually
Check the generated chart to ensure the shape and dimensions match your input.

Why go through all this trouble? Why not just treat everything like a square?

Feature	Regular Shape	Irregular Shape
Typical Use	Textbook problems	Real-world layouts (Rooms, Land)
Formula	Single formula (e.g., L ×W)	Multiple formulas combined (Decomposition)
Measurement	Simple (measure 1 or 2 sides)	Complex (measure all sides/diagonals)
Accuracy	Very High	Variable (depends on method used)
Examples	Square, Circle, Rectangle	Freeform Garden, L-Shaped Room

Calculating the area of an irregular shape becomes easy once you pick the right method.

• Decomposition: Best for building and DIY. Break it into simple shapes.
• Grid Counting: Best for nature and curves. Count the squares.
• Coordinate Geometry: Best for surveying. Use the precise formula.

✅ Don’t forget: Scroll up to use our Irregular Shape Area Calculator to get instant results, visualize your shape, and avoid manual math errors.

The information and tools provided in this guide, including the Irregular Shape Area Calculator, are intended for educational and estimation purposes only. While the underlying formulas are mathematically accurate, real-world conditions and measurements may vary. For legal, regulatory, or official applications, such as property boundaries or land surveys, consult a licensed professional surveyor.